
前置芝士:并查集,图论根本,数论根本1x0f 简介
实在最小生成树只是某个人用来装*的 —— 某老师

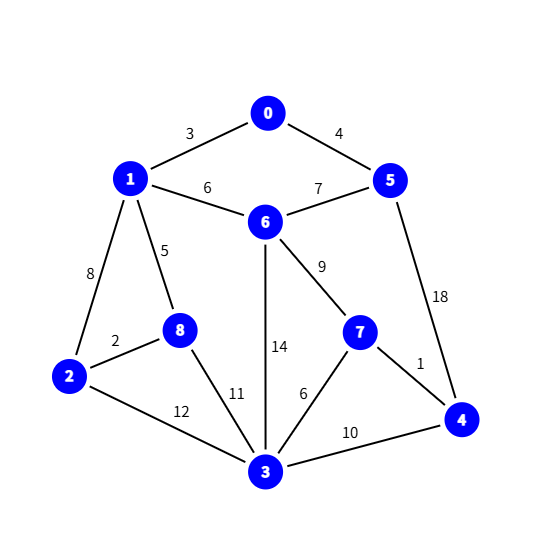
那么我们发现,这个方法需要两种操作:
- 按照边权排序
- 选择边7-4,连通7,4
- 选择边2-8,连通2,8
- 选择边1-0,连通1,0
- 选择边0-5,连通0,5
- 选择边1-8,连通1,8
- 选择边1-6,连通1-6
- 选择边3-7,连通3,7
- 选择边6-5,但是由于6,5已经连通,以是可以不加此边
- 选择边1-2,但是由于1,2已经连通,以是可以不加此边
- 选择边6-7,连通6,7
- 已经形成一棵树,后面的边都不选了
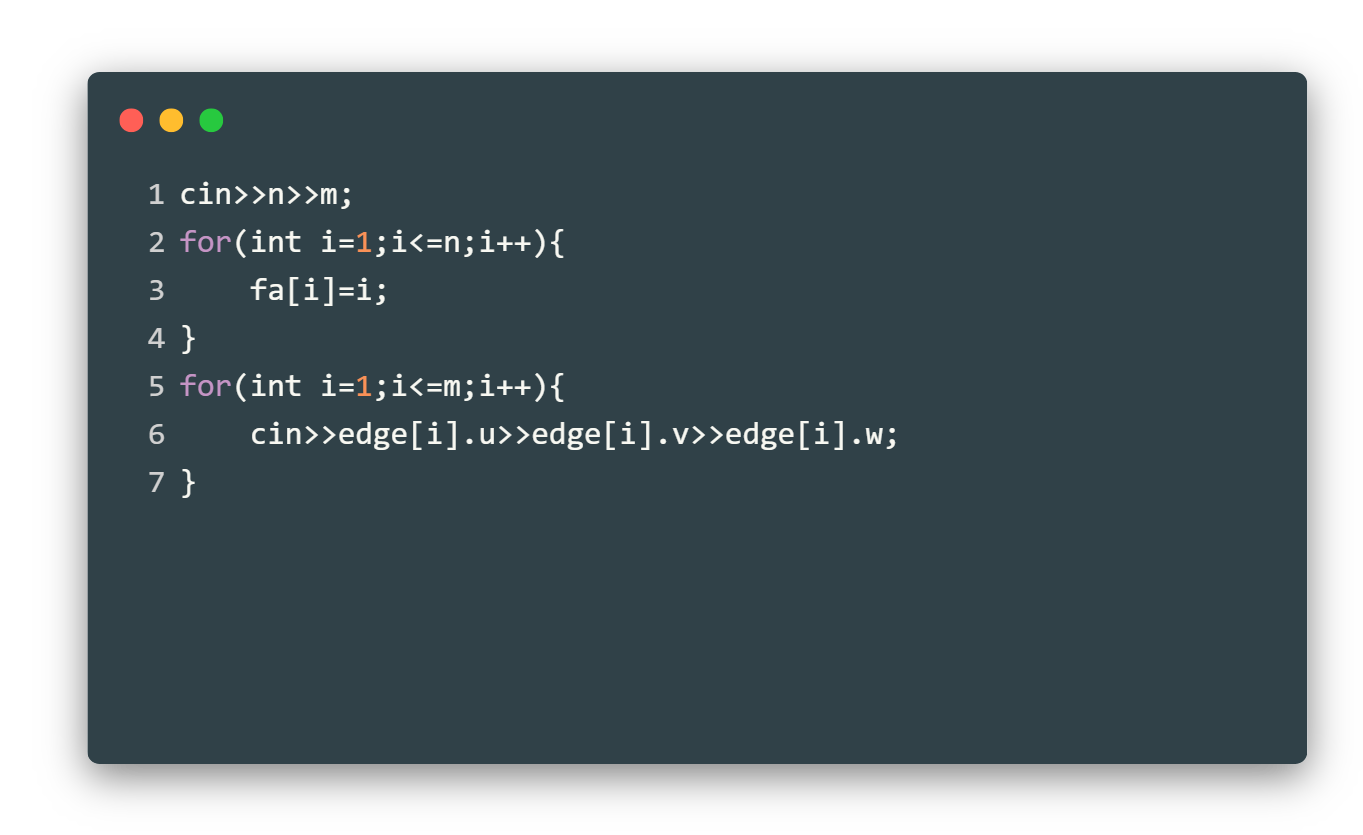
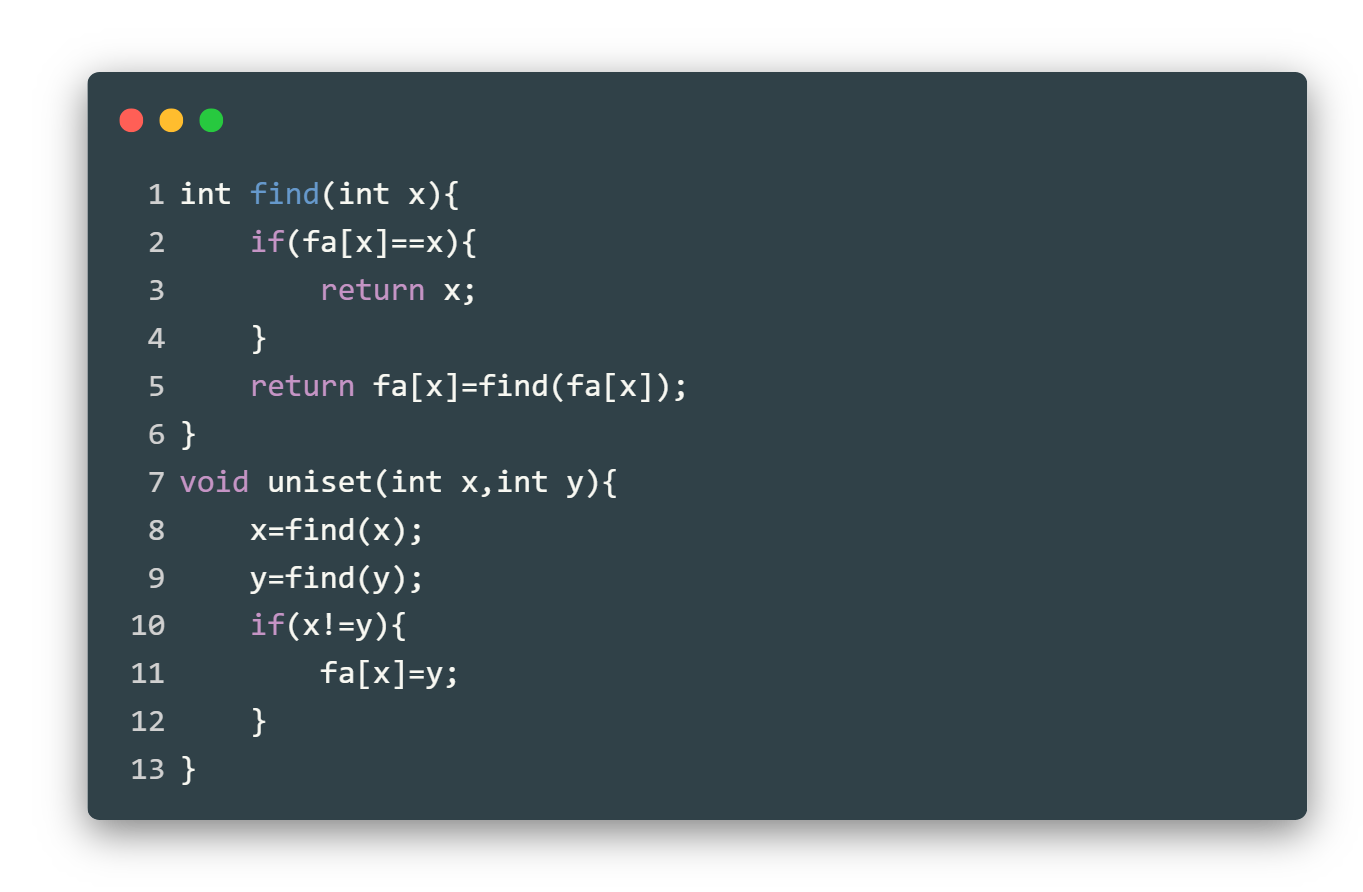
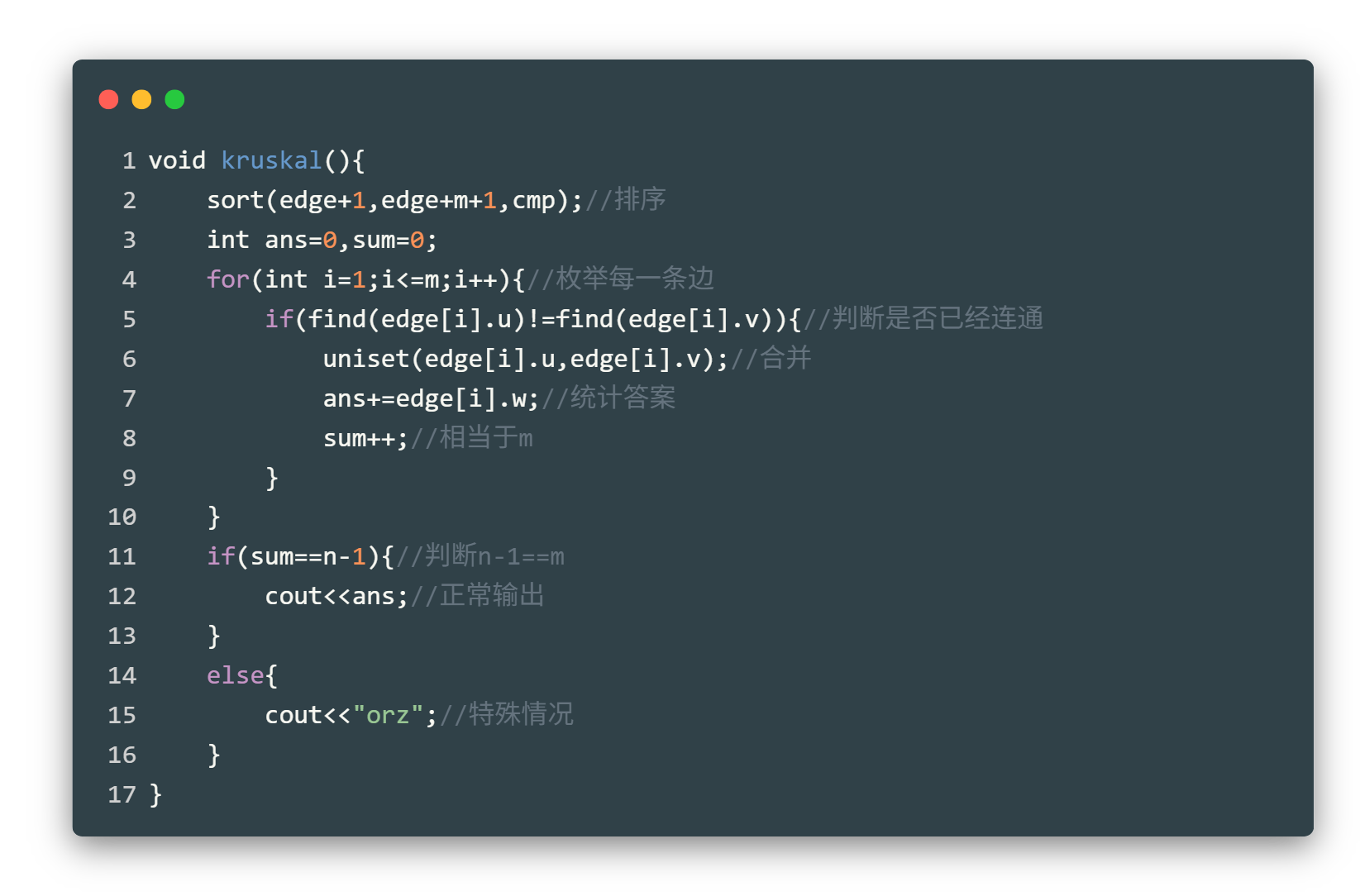
| 欢迎光临 qidao123.com技术社区-IT企服评测·应用市场 (https://dis.qidao123.com/) | Powered by Discuz! X3.4 |