


为什么就用一个hash函数不可?假设布隆过滤器中的hash函数满意simple uniform hashing假设:每个元素都等概率地hash到m个位中的任何一个,与别的元素被hash到哪个位无关。那么
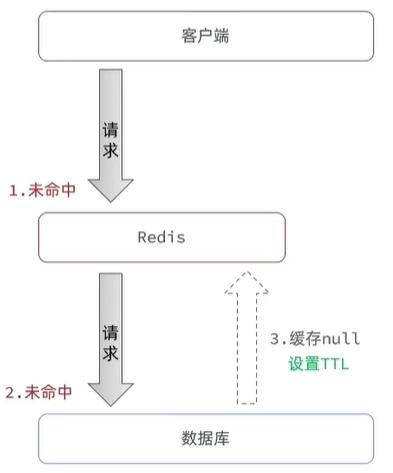
其实布隆过滤器底层是用 位图 实现的,而多个hash函数就是为了减少位图的误判率的。详细可往下看

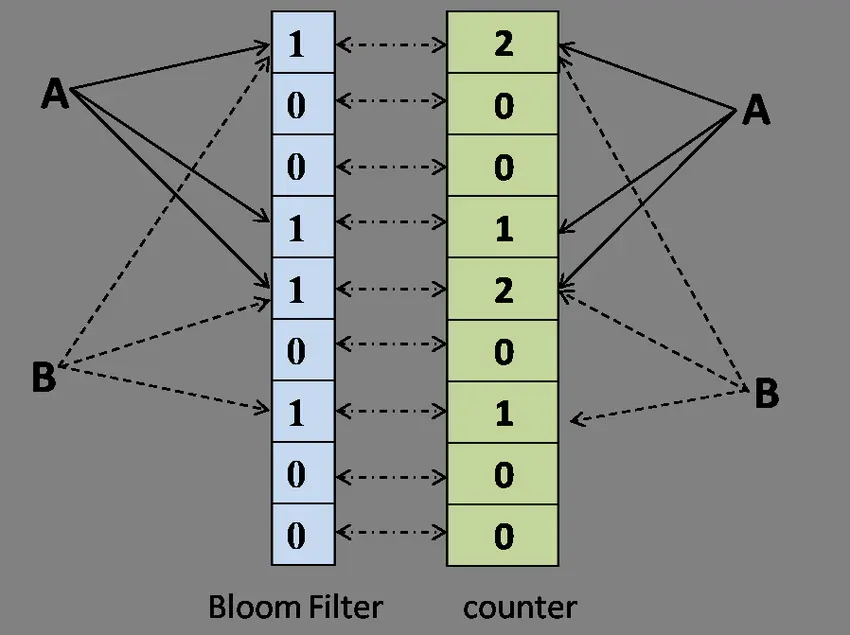


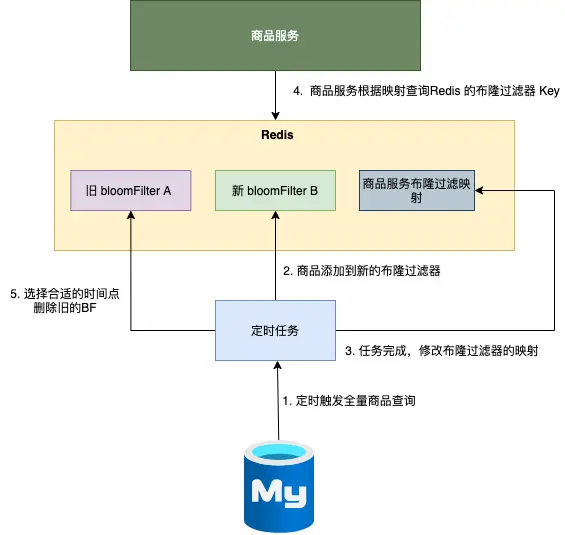
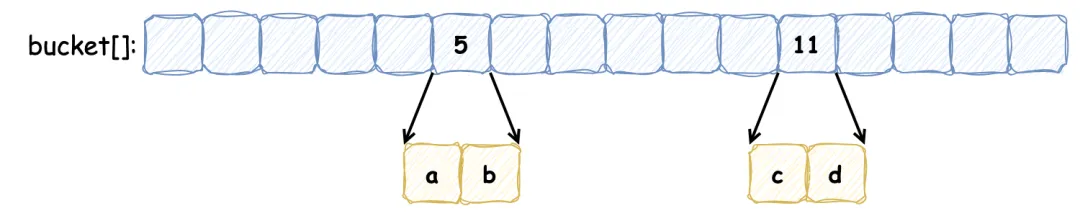
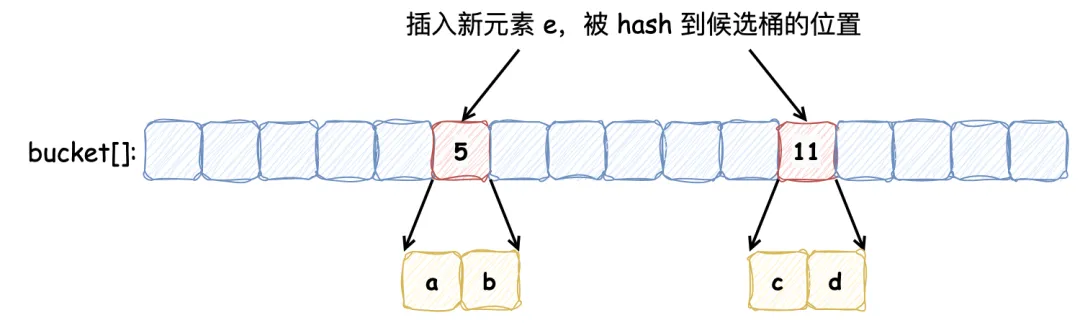
布谷鸟过滤器之所以被称为“布谷鸟”,是因为它的工作原理类似于布谷鸟在天然界中的举动。布谷鸟以将自己的蛋产在其他鸟类的巢中而闻名,如许一来,寄主鸟就会抚养布谷鸟的幼鸟。布谷鸟过滤器本质上是一个 桶数组,每个桶中保存多少数量的 指纹(指纹由元素的部门 Hash 值盘算出来)。定义一个布谷鸟过滤器,每个桶记录 2 个指纹,5 号桶和 11 号桶分别记录保存 a, b 和 c, d 元素的指纹,如下所示:
在布谷鸟过滤器中,如果一个位置已经被占用,新元素会“驱逐”现有元素,将其移到其他位置。这种“驱逐”举动类似于布谷鸟将其他鸟蛋推出巢外,以便安置自己的蛋。因此,这种过滤器得名为“布谷鸟”过滤器。

| 欢迎光临 qidao123.com技术社区-IT企服评测·应用市场 (https://dis.qidao123.com/) | Powered by Discuz! X3.4 |